たまには確率の話を。
目次
はじめに
モンティ・ホールの問題という有名な数学の問題があります。
これは、モンティ・ホールという人が司会者をしていたテレビ番組で行われた、賞品ゲームに関する問題です。
当時アメリカで、IQ世界一でギネスブックに登録されたマリリン・ボス・サヴァント(IQ228)という女性が、「Parade」という雑誌に読者からの質問に答えるというコラム「マリリンにおまかせ」を連載していました。
そして、この賞品ゲームに関する質問が読者から投稿されたので、サヴァント女史がコラムで解説したのですが、その回答を巡って「でたらめを言うな」と10,000通以上の反論が殺到し、しかもその中の1,000通は数学者や博士号保持者によるものであったことから大騒動に発展したという問題です。
影響に驚いたサヴァント女史は連載コラムを3回も使ってあの手この手で解説をするのものの、批判は鳴りやまず大騒動になるのですが、サヴァント女史は最後まで見解を変えません。
そして、最終的にはサヴァント女史の見解が正しいことが分かったという問題です。
問題
ゲームはシンプルで、3つの扉があり、1つを開けると商品があり(当たり)、残りの2つは何もない(ハズレ)というものです。
自分が賞品を懸けて、3つの中から扉を1つ選ぶという賞品ゲームです。
しかし、それだけではないところがみそです。
1.自分が扉を1つ選ぶ。まだ開けない。
2.司会者が残りの2つからハズレの扉を1つ開ける。
3.自分はもう一度扉を選べる。
というゲームです。
具体的に言うと、自分はAを選んだら、司会者が「これはハズレでした」と言ってCを開け、「今ならBに変えてもいいですよ」と聞くというもの。
この時、変えるべきか変えないべきか、ある人がサヴァント女史に聞いたわけです。
サヴァント女史の答えは、変えた方が当たる確率は2倍になるから変えた方がよい、というものでした。
しかし、上記の例だと、司会者がCはハズレと言って開けてしまったので、自分はAのドアノブを握っていますが、AかBか完全に2択であり、当たる確率はどちらにしても1/2のように感じる方が素直と思います。
それゆえ、大論争になった問題であり、結論があまりに直観に反することから、モンティ・ホールのパラドクスとかモンティ・ホールのジレンマなどといわれたりします(数学的に正解があるのでパラドクスではない)。
なお、この問題は、コンピューターで数百万回とか数億回とかシミュレーションしてみる方法が可能であり、変えた方が成功確率が2倍であることが、実験的に証明されています。
2つの戦略
結論を理解するためには、ゲームを通しで考えた方がよいです。
つまり、最初からこのゲームに参加するとしたら、どういう戦略で行くべきかを考えるというものです。
一番最初はあてずっぽうで選ぶ以外の余地はないので、このゲームには2つしか戦略はありません。
1.扉を変更しない(維持戦略)
2.扉を変更する(変更戦略)
まずは、維持戦略。
この場合、途中で司会者がハズレの1つを教えてくれたところで、自分の選択は変えないわけですから、最初にあたりを引くしかありません。
そして、あてずっぽうで当たりを引く確率は1/3です。
したがって、維持戦略の成功確率は1/3です。
次に、変更戦略。
変更戦略の場合、最初に当たりを掴んでしまうと、残りの(ハズレ、ハズレ)のうちどちらを司会者が開けようと、自分は当たりからハズレに変えるので、必ず外れることになります。
その一方で、もし自分が最初にハズレを掴むと、残りは(当たり、ハズレ)の組み合わせであり、司会者はそのうちのハズレを必ず開けるわけですから、必ず当たりが残り、その扉に変更するわけですから、必ず当たりになります。
つまり、変更戦略の場合、最初にあたりを掴めば(確率1/3)必ず外し、最初にハズレを掴めば(2/3)必ず当たることになります。
したがって、1/3×0 + 2/3×1 = 2/3であり、変更戦略の成功確率は2/3となります。
以上より、このゲームは、始める前から維持戦略より変更戦略の方が当たる確率が高いことは分かっています。
したがって、テレビ番組中に行われるゲームに参加する前日の時点で、変更戦略を貫徹する決心をするのが合理的で、選んだ扉を変更する方が当たる確率は高いことになります。
自分としては、当日にどの扉を選ぶかとか司会者がどの扉を開けたかに関係なく、選んだ扉から残ったもう1つの扉に変更した方が良いわけです。
なぜ、パラドクスと言われるのか
上記の理屈は分かったとしても、心では理解できないからこそこの問題は有名であり、パラドクスのような扱いを受けます。
ポイントは、自分がAを選んで、司会者がCを開けて、今ならBに変えてもいいですよと言った時の心理です。
時分としては、「Aかな、Bかな」と完全に2択ですから、どっちを選んでも当たる確率は1/2であると感じるのが自然です。
しかもややこしいことに、ゲームの最初に司会者がCを開けてくれてAとBのどちらでしょうかと言えば、ただの2択問題であり、数学的にもどちらも当たる確率は1/2です。
しかし、自分がAのドアノブを持った状態で、司会者がCを開けて、AかBかと聞く場合には、Aの確率は1/3で、Bの確率は2/3となります。
意思決定としては、AかBか2択なのに、最初に司会者がCを開けた場合と、自分があてずっぽうにAを選んだ後に司会者がCを開けた場合では、確率が変わるわけです。
ここが難しいから、パラドクスであるかのような扱いをされたりします。
この問題の最大のポイントは、司会者の行動の意味です。
司会者がハズレを1つ開けるという行為が無ければ、完全に3択問題であり、確率は1/3です。
しかし、司会者の行動が登場することで、変更戦略を取り、2/3の確率で当たるゲームになるということは、司会者は自分を助けてくれていることになります。
実は、司会者の行動は自分にとってヒントなわけです。
そこを考えてみます。
司会者の行動の意味
まず、司会者の行動が無い純粋な3択クイズを考えます。
3つの扉の中から、「A」とか「B」とか「C」とか一つを選ぶだけなら、確率は1/3です。
ではもし、「AとBのどちらか」、「AとCのどちらか」、「BとCのどちらか」と、2つの扉を選んでその中に当たりの扉があれば賞品をもらえるとした場合、このゲームの難易度はどう変わるでしょうか。
言わなくてもわかるように、ゲームは簡単になります。
扉を2つ選べるわけですから、1つ選ぶ場合と比較して確率は2倍になり、当たる確率は2/3になります。
自分の選択肢は「AとB」、「AとC」、「BとC」の3つですが、当たりがA,B,Cのどれであれ、3つ中2つは正解ですから、そう考えても当たる確率は2/3です。
実は、モンティー・ホール問題というのは、扉を2つ選ぶのと同じことなのです。
扉は3つしかないわけですから、Aを選ぶというのは、「BとC」を選ぶのと同じことを意味します。
そして、BとCの中から、ハズレの1つを司会者が取り除いてくれます。
自分が、当たりは「BとC」のなかのどちらかだと思えば、最初にAを選べばよく、残ったBとCの中からハズレを司会者が消してくれます。
そして、残った方に変更すればいいわけです。
つまり、最初にAを選ぶとしても、司会者がBとCのなかからCを消して、自分はBに乗り換えるというのは、最初から「BとC」のどちらかに当たりはある、といってゲームをしているのと変わりません。
2つの扉を選ぶ場合、2/3の確率で「当たり、ハズレ」の組み合わせになり、その内のハズレは司会者が教えてくれますから、2/3の確率で最終的に当たりにたどり着けます。
逆に言うと、1/3の確率で「ハズレ、ハズレ」という組み合わせを引いたときだけ、司会者の行動は何の役にも立たず、そのまま自分も間違えます。
その結果、変更戦略の成功確率は2/3なわけです。
以上のように、1つだけ選ぶより2つ選ぶ方が間違いなく有利なわけですが、「自分が選ばなかった2つの扉の中から司会者がハズレを1つ教えてくれる」という行動によって、3択をしているようで、その実、自分は最初に2枚選ぶことが可能になっているわけです。
司会者の行動により、純粋3択して途中で意見を変えているのではなく、最初から2枚選ぶゲームをしていることになります。
結果として、司会者の行動があるお陰で、単純な3択以上の有利な戦略を取れるようになっています。
つまり、司会者の行動には、自分を助けてくれているわけです。
別の言い方をすると、「自分がAを選んだ状況で司会者がCを開けた」というのは、自分にとって利用可能で、価値のある情報であるということになります。
情報としての価値
上記の話を情報の価値という観点から整理しなおします。
自分がAを選んだら、司会者がこれはハズレと言ってCを開けた。
その時点で、AとBの2択のような気がしますが、これが2択ではないというのはどういうことか。
結論から言うと、目の前にあるAとBは全く同じ見える扉のようでもそうではないということです。
Aは1/3の確率で当たる扉であり、Bは2/3の確率で当たる扉なわけです。
その場合、2/3の確率で当たるBを選んだ方が有利なのは明らかです。
つまり、Bには、一流数学者のみに見える光のオーラがかかっており、より当たりやすい扉になっているわけです。
では、その光のオーラはいつ登場したのか。
当然、司会者がCを開けたときです。
最初は、AもBもCも普通の扉です。
しかし、司会者がCを開けた瞬間に、Bに光のオーラが登場し、当たりやすい扉に変化します。
これが分かりにくい。
もし、自分が最初にAを選んで、司会者がCを開け再検討を促し、自分はAのドアノブを離し、AとBの間で迷っているとします。
そのタイミングで、いきさつを知らない天才数学者が登場しても、その人から見れば当たりはAかBのどちらかであり(確率は1/2)、Bの扉の光のオーラは見えません。
「自分がAを選んだ状況で司会者がCを開けた」という情報を知っている人だけに、Bの扉は特別なものとなります。
別の言い方をすれば「自分がAを選んだ状況で司会者がCを開けた」という情報には自分を助ける価値があるのです。
それはなぜか。
司会者は完全にランダムに行動しているわけではなく、自分の行動の結果として必然的な行動をとらざるを得なかった可能性があるからです。
自分がAのドアノブを握ったら、次の司会者の行動を凝視します。
この時、司会者はAの扉は開けられないので、考えられる司会者の行動と確率は下記です。
1.Aが当たりで、適当にBを開ける => 1/3×1/2=1/6
2.Aが当たりで、適当にCを開ける => 1/3×1/2=1/6
3.Bが当たりで、Cを開けるしかない => 1/3×1=1/3
4.Cが当たりで、Bを開けるしかない => 1/3×1=1/3
そうしたら、司会者がCを開けた。
ということは、考えられる状況は上記の2.と3.しかないわけですが、確率1/6と1/3で、3.である可能性が2倍なわけです。
司会者が何もしなければ、当たりは、A,B,Cそれぞれ1/3の確率です。
しかし、司会者がCを開けたということは、Cが当たりの可能性が消えただけでなく、1/6の可能性を持っていた1.つまり、Aが当たりで適当にBを開けるという可能性まで消えたわけです。
つまり、「自分がAのドアノブを持った状態で司会者がCを開けた」という情報は、Cである可能性だけでなく、Aである可能性も半分減らしてくれたわけです(ここが肝)。
以上より、司会者がCを開けたら、その情報を生かして、Bが当たりである可能性に懸ける方が当たる確率は2倍になると言えます。
バックトゥザフューチャー
バックトゥザフューチャー的に考えてみます。
司会者がCを開けた時点で、自分はどの未来にいるのかを考えてみます。
まず、過去をさかのぼって考えてみます。
今から考えるとAのドアノブを握った時点で未来は4つに分岐したはずです。
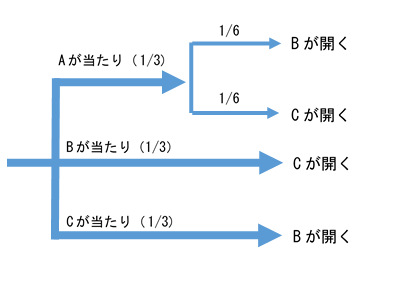
起こりうる可能性が異なるためその4つは対等ではありません。
司会者がCを開けたことにより、Aが当たりの未来か、Bが当たり未来のどちらかに来ていることは分かったのですが、実はその未来の2本の線は太さ(発生する確率)が違います。

この場合に、自分がどの未来にいる可能性に懸けるかと言えば、当たりがBの未来にいる可能性が2倍高いわけです。
今この瞬間がどちらかは分からないわけですが、9999回やれば、6666回はBが当たりのはずなわけです。
したがって、今はBが当たりである未来にいる可能性に懸ける方が合理的と言えます。
この例え話いらなかったかな。
でも、確率と統計のつながりこそが分かりにくいともいえるので消さないでおこう。
おわりに
有名なモンティ・ホール問題について解説してみました。
ネットでは様々な解説記事がありますが、一番わかりやすい記事を目指しましたが、どうなることやら。
それどころか、専門家ではないので間違っていたらすみません。
場合の数・確率はかなり得意な方だったんだけどなあ。
まあ、大学入学以降はほとんど触れていないのでその程度でもあります。
